More Robust ITS

Adversarial attacks and defenses against deep learning–based traffic forecasting.

This project explores adversarial vulnerabilities of deep learning–based traffic forecasting and the effective mitigation strategies, which is composed of the following publications:

1. Adversarial Danger Identification for Traffic Forecasting

Research gap

  • However, Deep Neural Networks (DNNs) have been widely proven to be vulnerable to carefully crafted perturbations. For instance, recent studies have rigorously demonstrated that state-of-the-art GNN-based traffic forecasting models can be easily misled by small manipulations, resulting in the breakdown of the traffic system.

  • The shown vulnerabilities of state-of-the-art forecasting models cast into question the usability and reliability of DNNs in real-world applications. It is thus imperative to develop effective methods to protect these models.

  • Though researchers have proposed two types of adversarial defense strategies—re-training and filtering—to protect DNNs in various static applications, these methods are not applicable to time series applications.

    • First, re-training-based strategies typically modify the internal components or structures of DNNs. For instance, adversarial training, a typical re-training-based method, adds adversarial perturbations or random noises to the training dataset to enhance DNNs’ robustness. However, re-trained models are still vulnerable to advanced adversarial attacks or new datasets. Furthermore, state-of-the-art forecasting models’ parameters and training settings are carefully designed, making it difficult to restore their original performance if these models are re-trained. Thus, re-training is not a viable option for protecting GNN-based forecasting models in forecasting domains.

    • Second, filtering-based defense strategies are designed to cleanse the poisoned input by removing local features while preserving the object’s global structure. Static DNN-based classification models can work effectively with low-dimension features; yet filtered inputs could significantly compromise the model’s forecasting performance.

Solution

The key idea to address the contradiction issue is to design a filter that only works on selected data, temporally and by variate, instead of the entire dataset so that the original local features in most data are not distorted. The underpinning assumption behind the aforementioned idea is that a forecasting model’s vulnerability is not static; it is temporally and variate-wisely dynamic.

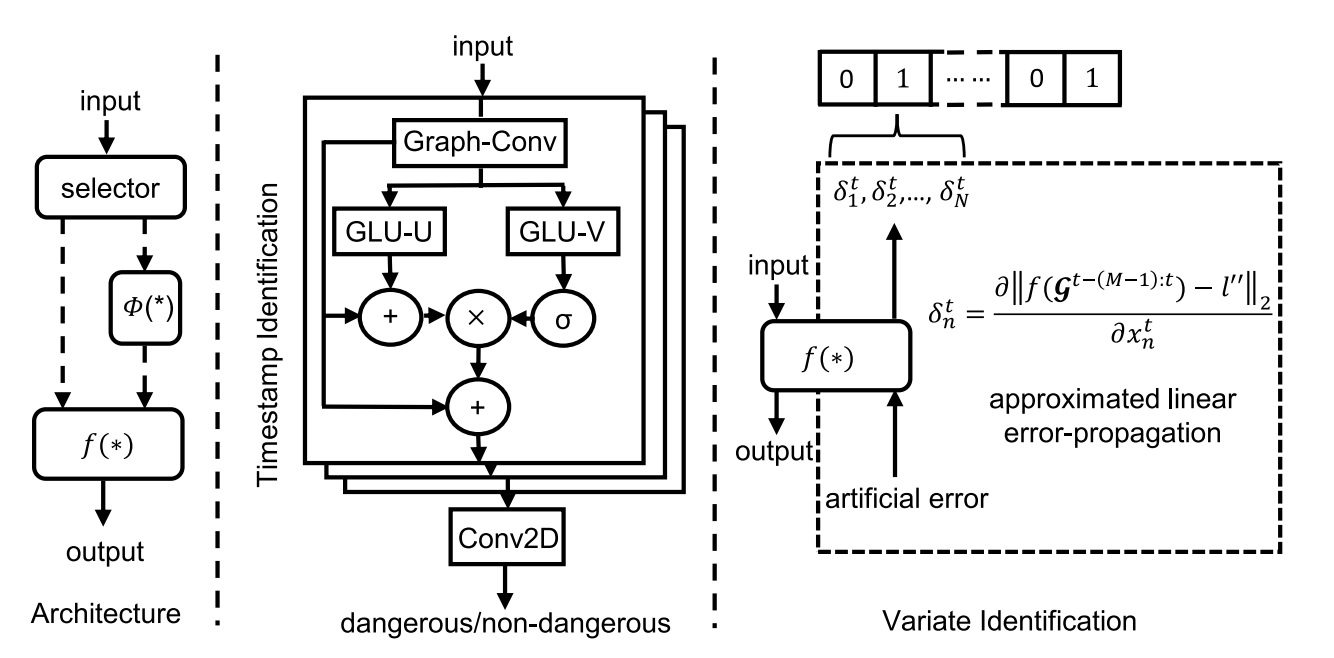
The overall architecture of ADI-TDG is composed of a filter and a selector.

Hybrid GNN for Timestamp Identification.

The timestamp identification is to identify when attacks on the forecasting model are likely to cause disproportionately large errors.

We formulate identifying dangerous timestamps as a time series classification problem; a hybrid GNN-based classifier is designed to tackle the problem. The inputs to the classifier are those fed into the forecasting model; the outputs are labels indicating whether an adversarial attacker can severely fool the forecasting model for a specific frame.

  • Let $l^{‘,t}$ denote the label to the classifier in the $t$ timestamp, and these labels are computed as:
\[l^{',t}=\begin{cases} 1, & \|f(\mathcal{G}^{t-(M-1):t}+\rho) - l^t\|_1 > \lambda \cdot N\\ 0, & \|f(\mathcal{G}^{t-(M-1):t}+\rho) - l^t\|_1 \le\lambda \cdot N. \end{cases} \tag{1-1}\]

  • The classifier is constructed with three graph-temporal modules and a 2D convolutional layer. Each graph-temporal module is composed of a graph convolution layer and a gate-based 1-D dilated convolutional layer.

  • The graph convolutional layer is applied to embedding correlations between variates. Supposing that $*_g$ denotes the graph convolution, $s_j$ denotes the input to the $j$th graph-temporal module, and $\Theta$ denotes the parameters of graph convolutional kernel computed from the adjacency matrix. The output of the graph convolutional layer in the $j$th graph-temporal module, $s’_j$, is computed as:

\[s'_j= \Theta *_{g}s_j. \tag{1-2}\]
  • The output of the graph convolutional layer goes into the 1-D dilated convolutional layer constructed with the gated linear unit (GLU). Supposing that $\Gamma$ denotes the kernel for 1-D convolution, $\otimes$ denotes the 1-D convolution operation, $[U,V]$ denotes the set of two intermediate outputs of the 1-D dilated-CNN, $\odot$ denotes the Hadamard product, $\mathcal{P}(s’_j)$ denotes sampling the input channel to be as same as the intermediate output $U$, and $\sigma(\cdot)$ denotes the sigmoid function, the output of GLU in the $j$th graph-temporal layer, $r_j$, is computed as:
\[r_j=\Gamma \otimes s'_j=(U+\mathcal{P}(s'_j))\odot \sigma(V). \tag{1-3}\]
  • The said two intermediate outputs, $[U,V]$, are split in half of the size of the graph convolutional layer’s output channel. Let $\Theta_{1}$ and $\Theta_{2}$ be the parameters of the convolution kernels, $\mathbf{b}$ and $\mathbf{c}$ be the bias, $\star$ be the dilated convolutional operation, and $[s’_U,s’_V]$ denotes the equally split outputs from the graph convolutional layer. The two intermediate outputs are computed as:
\[\begin{cases} U=\Theta_{1}\star s'_{U}+\mathbf{b}\\ V=\Theta_{2}\star s'_{V}+\mathbf{c}. \tag{1-4} \end{cases}\]
  • Identifying when is dangerous is formed as a time series classification problem. A hybrid GNN-based classifier is designed to identify whether a timeframe needs adversarial defenses. The proposed classifier, $\mathcal{C}$, parameterized by the coefficient set, $w$, is learned in the training dataset following:
\[\mathop{\min_{w}}=\|\mathcal{C}(\mathcal{G}^{t-(M-1):t},w)-l^{',t}\|_2. \tag{1-5}\]

Linear Error Propagation for Variate Identification.

While the aforementioned classifier can identify when to defend, this part presents the method to identify the variates to defend. Analogous to the case of timestamps, filtering all variates in the dangerous timestamp is not advisable because the forecasting model’s vulnerability varies by variate. Based on this idea, this part proposes an approximate linear error propagation (ALEP) to identify the exact variates to protect, namely ``where to protect”.

  • The key idea is to utilize the DNN’s high-dimension linearity to describe the correlation between a forecasting model’s prediction errors and perturbations added into inputs. Specifically, well-designed unnoticeable noises can diffuse into many of the DNN’s outputs and accumulate to be extremely large errors through the DNN’s high-dimension mapping.

  • The proposed Approximate Linear Error Propagatio (ALEP) is to compute the ratio of prediction errors to added perturbations. With a larger ratio, an added perturbation can lead to a greater prediction accuracy drop, and consequently, variates with a large ratio are regarded as ``dangerous”. The said ratio, which is represented as $\delta^t_n$ for the $n$th variate in timestamp $t$, is computed as

\[\delta^t_n =\frac{\partial \|f(\mathcal{G}^{t-(M-1):t})-l^{'',t}\|_2}{\partial x_n^t}. \tag{1-6}\]
  • In Equation (1-6), $l^{‘‘,t}$ denotes the artificial label and it is designed as:
\[l^{'',t}=\mathcal{G}^t+\beta. \tag{1-7}\]
  • In Equation (1-7), $\beta$ denotes the bias factor to tune the scale of artificial errors and it is computed from the training dataset, which is shown as:
\[\beta = {\rm mean} \{f(\mathcal{G}^{t-(M-1):t}+\rho)-\mathcal{G}^t\}. \tag{1-8}\]
  • The computed ratio represents the degree of errors that perturbations can cause. A larger ratio means perturbations can cause greater damage to the forecasting model if it is fed into the specific variate. Variates with the computed ratio greater than the threshold, $\bar{\delta}$, are regarded as vulnerable. The threshold is computed as:
\[\bar{\delta} = \min\{\frac{\partial \|f(\mathcal{G}^{t-(M-1):t})-l^{t}\|_2}{\partial x_n^t}\}. \tag{1-9}\]

Scatter Filter.

The scatter filter is used to replace the possible perturbations with dispersion errors. The key idea is that the dispersion errors can lead to less prediction accuracy drop compared with well-designed adversarial perturbations.

Supposing that $x$ denotes the input to the scatter filter, $[\cdot]$ denotes the normal rounding operation, and $k$ denotes the factor to tune the scale of input, the scatter filter, $\Phi(\cdot)$, is designed as：

\[\Phi(x)=[k \cdot x]. \tag{1-10}\]