More Accurate ITS

Two model-agnostic solutions to improve deep learning–based traffic forecasting.

This project explores model-agnostic approaches for enhancing the performance of deep learning–based traffic forecasting, which is composed of two publications:

1. Autocorrelated Error Adjustment for Traffic Forecasting

Research gap

Mean squared error (MSE) estimation is frequently misapplied in the training of deep learning–based numerical forecasting models. Specifically,

  • Most existing studies treat forecasting tasks as regression problems and adopt standard regression training frameworks to optimize forecasting models.
  • Suppose each training example is denoted by a pair $\langle x, y \rangle$, where $x$ represents the input features and $y$ the corresponding target. The goal of regression is to learn a function $f$ that models the conditional distribution $p(y \mid x)$. A widely used approach is maximum likelihood estimation (MLE), which seeks to maximize the likelihood of the observed data under the model distribution. Assuming errors follows a Gaussian distribution with variance $\sigma^2$, the general form of the MLE loss function is:
\[\mathcal{L}_{\text{MLE}} = -\sum_{i=1}^n \log p(y_i \mid x_i; f) = \frac{1}{2\sigma^2} \sum_{i=1}^n \left( y_i - f(x_i) \right)^2 + \frac{n}{2} \log(2\pi\sigma^2). \tag{1-1}\]
  • When the errors are assumed to be independent and identically distributed (i.i.d.), the variance term $\sigma^2$ becomes constant. In this case, maximizing the likelihood is equivalent to minimizing the mean squared error (MSE), which simplifies the training objective:
\[\mathcal{L}_{\text{MLE}} \sim \mathcal{L}_{\text{MSE}}=\sum_{i=1}^n \left( y_i - f(x_i) \right)^2 = \| y - f(x) \|_2^2. \tag{1-2}\]

  • MSE is simple, computationally efficient, and widely used in practice. In standard regression tasks, where training samples are typically assumed to be randomly drawn from a distribution, the i.i.d. assumption holds reasonably well.

  • Existing time series forecasting studies adopt this same regression-based training paradigm, implicitly relying on the i.i.d. error assumption. However, Adjusting for Autocorrelated Errors in Neural Networks for Time Series (NeurIPS 2021) was among the first to question this assumption in univariate forecasting, showing that autocorrelated errors in the temporal dimension can negatively affect forecasting performance. Our work builds upon this insight and extends the discussion to the multivariate case, where spatial and temporal correlations in errors are even more prominent.

Solution

Model forecasting errors as a Vector Autoregressive (VAR) process instead of the i.i.d. assumption.

  • Supposing $\epsilon_t$ represents the prediction error, traditional forecasting methods assume prediction errors are independent and identically distributed (i.i.d), typically $\epsilon_t \sim \mathcal{N}(\mathbf{0}, \Sigma)$. A one-step-ahead traffic forecasting model is typically formulated as:
\[\mathcal{G}_{t} = f\left(\mathcal{G}_{t-1},...,\mathcal{G}_{t-H};\theta \right) + \epsilon_t. \tag{1-3}\]

  • The model is often trained by minimizing the loss functions $\text{MSE} \sim \sum\nolimits_t{|\epsilon_t|_2}$ and $\text{MAE} \sim \sum\nolimits_t{|\epsilon_t|_1}$, which correspond to independent Gaussian and independent Laplacian noise assumptions, respectively.

  • The independent noise assumption does not hold in real-world traffic forecasting, to account for spatiotemporal autocorrelation, we redefine the error term $\epsilon_t$ as $\eta_t$:

\[\mathcal{G}_{t} = f\left(\mathcal{G}_{t-1},...,\mathcal{G}_{t-H};\theta \right) + \eta_t. \tag{1-4}\]
  • In Eq.(1-4), $\epsilon_{t} \sim N(\boldsymbol{0},\Sigma)$ is a Gaussian white noise process, and $\Phi_{1},…,\Phi_{p}$ are coefficient matrices of size $N\times N$. We define $\eta_t$ to follow a vector autoregressive process VAR($p$):
\[\eta_t = \Phi_{1}\eta_{t-1} + \dots + \Phi_{p}\eta_{t-p} + \epsilon_{t}. \tag{1-5}\]

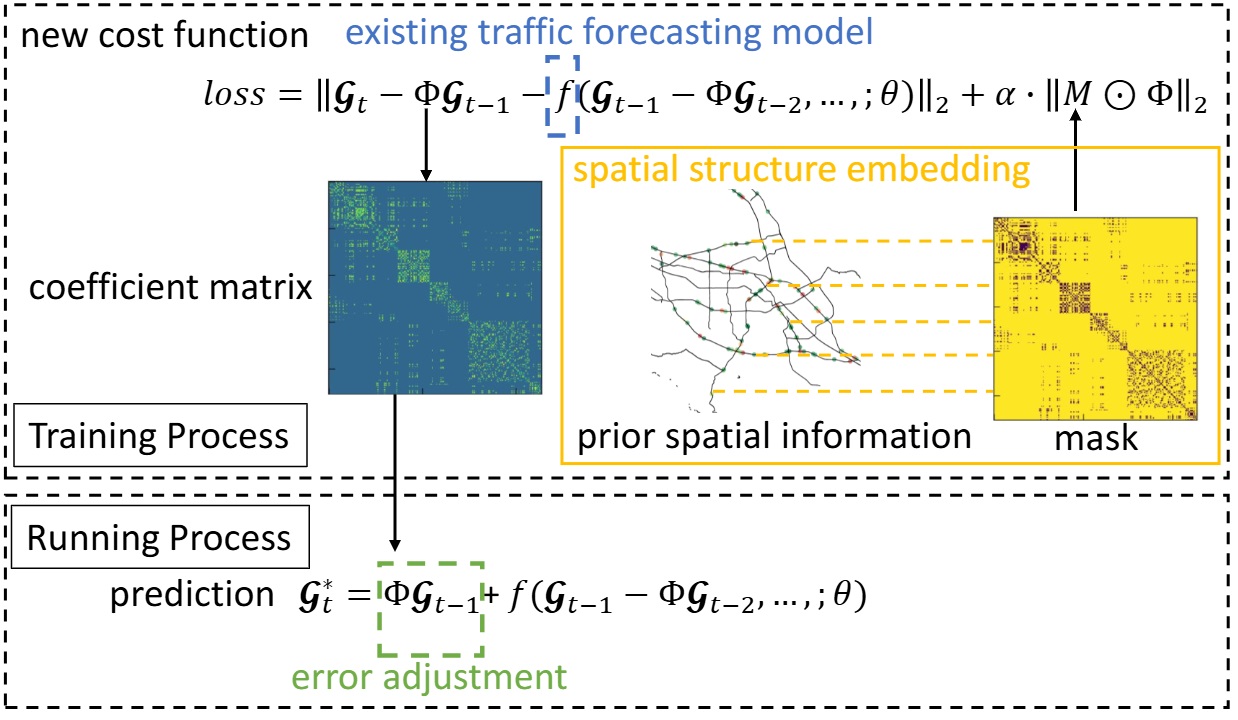
Redesign the loss function that explicitly incorporates spatiotemporal correlations.

  • To adjust for autocorrelated errors, we employ a VAR(1) model in DNN-based traffic forecasting. By combining Eq.(1-4) and Eq.(1-5), the updated traffic forecasting model is formulated as:
\[\mathcal{G}_{t} = f\left(\mathcal{G}_{t-1},...,\mathcal{G}_{t-H};\theta \right) + \Phi\eta_{t-1}+\epsilon_{t}. \tag{1-6}\]
  • The historical prediction error, $\eta_{t-1}$, is computed as:
\[\eta_{t-1}=\mathcal{G}_{t-1}-f\left(\mathcal{G}_{t-2},...,\mathcal{G}_{t-H-1};\theta \right). \tag{1-7}\]
  • Combining Eq.(1-6) and Eq.(1-7), we reformulate the traffic forecasting model as:
\[\mathcal{G}_{t} - \Phi\mathcal{G}_{t-1} = f\left(\mathcal{G}_{t-1},...,\mathcal{G}_{t-H};\theta \right) - \Phi f\left(\mathcal{G}_{t-2},...,\mathcal{G}_{t-H-1};\theta \right) + \epsilon_t. \tag{1-8}\]
  • This new formulation accounts for autocorrelated errors, but its complexity poses challenges in direct estimation. To simplify, we approximate the right-hand side of Eq.(1-8) as:
\[\mathcal{G}_{t} - \Phi\mathcal{G}_{t-1} = f\left(\mathcal{G}_{t-1}- \Phi\mathcal{G}_{t-2},...,\mathcal{G}_{t-H}- \Phi\mathcal{G}_{t-H-1};\theta \right) + \epsilon_t. \tag{1-9}\]
  • Now, minimizing the independent Gaussian error, $\epsilon_t$, in Eq.(1-9), the final cost function used for training is updated as:
\[loss = \left\| \mathcal{G}_{t} - \Phi\mathcal{G}_{t-1} - f\left(\mathcal{G}_{t-1}- \Phi\mathcal{G}_{t-2},\ldots,;\theta \right) \right\|_2 + \alpha \cdot\mathcal{R}. \tag{1-10}\]
  • Training with the new cost function, we can directly learn both the model parameter and the coefficient matrix.
The framework of the proposed Spatiotemporally Autocorrelated Error Adjustment.